在接下来的这篇文章中,我们将借助一个生动而具体的案例,带领读者深入探究机器学习的实际运作过程,清晰直观地让读者明白机器学习究竟是在进行怎样的工作,如何从海量的数据中挖掘出有价值的信息,如何通过不断的学习和优化来实现各种神奇的功能,从而让读者对机器学习有一个更为深刻和准确的认知。
机器学习的Hello world——鸢尾花识别
像大多数编程语言的入门教程一样,都是从输出Hello world开始,我们也从机器学习的Hello world问题开始。
鸢尾花数据集(Iris Dataset)是机器学习领域中一个非常经典且常用的数据集。
它包含了 150 个样本,分别属于三种不同的鸢尾花品种(山鸢尾 setosa、变色鸢尾 versicolor和维吉尼亚鸢尾 virginica)。每个样本有四个特征,分别是花萼长度(sepal length)、花萼宽度(sepal width)、花瓣长度(petal length)和花瓣宽度(petal width)。

现在让我们看一看这个数据集中的数据吧(下表),target列表示所属的品种,分别用0代表山鸢尾,1代表变色鸢尾,2代表维吉尼亚鸢尾,一共三个类别;id是序号,暂时可以不用管。
| id | sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target |
|---|---|---|---|---|---|
| 91 | 6.1 | 3.0 | 4.6 | 1.4 | 1 |
| 77 | 6.7 | 3.0 | 5.0 | 1.7 | 1 |
| 99 | 5.7 | 2.8 | 4.1 | 1.3 | 1 |
| 65 | 6.7 | 3.1 | 4.4 | 1.4 | 1 |
| 14 | 5.8 | 4.0 | 1.2 | 0.2 | 0 |
| 108 | 6.7 | 2.5 | 5.8 | 1.8 | 2 |
| 142 | 5.8 | 2.7 | 5.1 | 1.9 | 2 |
| 127 | 6.1 | 3.0 | 4.9 | 1.8 | 2 |
| 24 | 4.8 | 3.4 | 1.9 | 0.2 | 0 |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | 0 |
单变量模型
假设我们完全没有机器学习背景知识,那么我们怎么来解决这个问题呢?最简单的思路,是去找规律。我们先从最简单的规律开始,只看4个属性中的一个——花萼长度。我们猜测,三种花的花萼长度不一样!
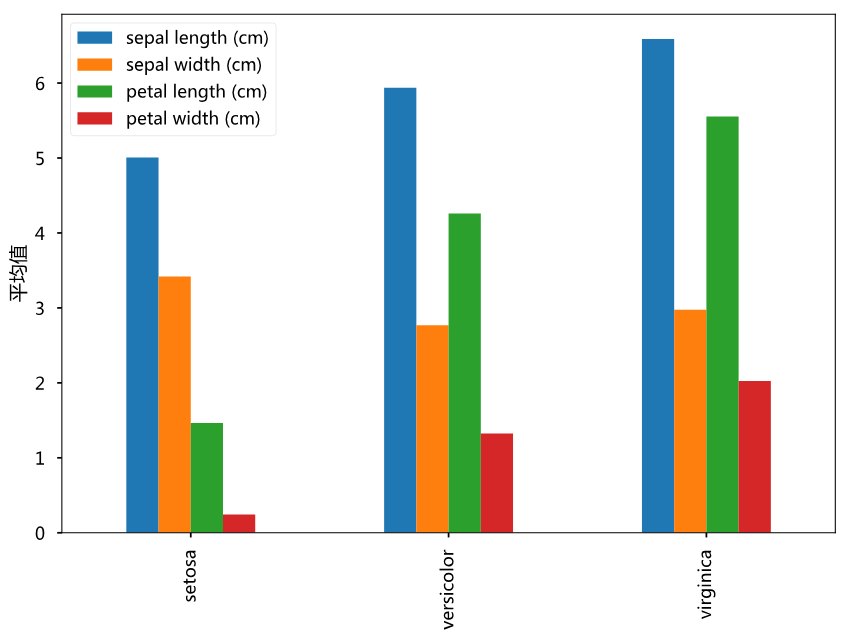
于是,我们简单计算了下3种花4个属性的平均值(如上图所示),结果发现每个属性确实都有一些差异,尤其是绿色的柱子(花瓣长度),差异最大。所以,我们根据平均值写下一个识别鸢尾花的算法
$$ target =
\begin{cases}
0, \text{petal length} \lt 2.8 \\
1, \text{petal length} \in [2.8, 4.9) \\
2, \text{petal length} \ge 4.9
\end{cases} $$
这个算法用Python实现非常简单:
def iris_classify(petal_length):
if petal_length < 2.8:
return 0
elif petal_length < 4.9:
return 1
return 2恭喜,我们实现了第一个机器学习模型——单变量的鸢尾花识别模型,是不是很简单。
决策树模型
前面的单变量模型可以用一棵决策树来表示出来,如下图所示。决策树是一棵二叉树,它是一种类似树状的结构,由节点和分支组成。决策树的根节点是整个模型的开始,然后通过对数据特征的不断判断和分支,形成多个子节点和分支,直到到达叶子节点,每个叶子节点(下图中方形结点)代表一个分类结果或预测值。
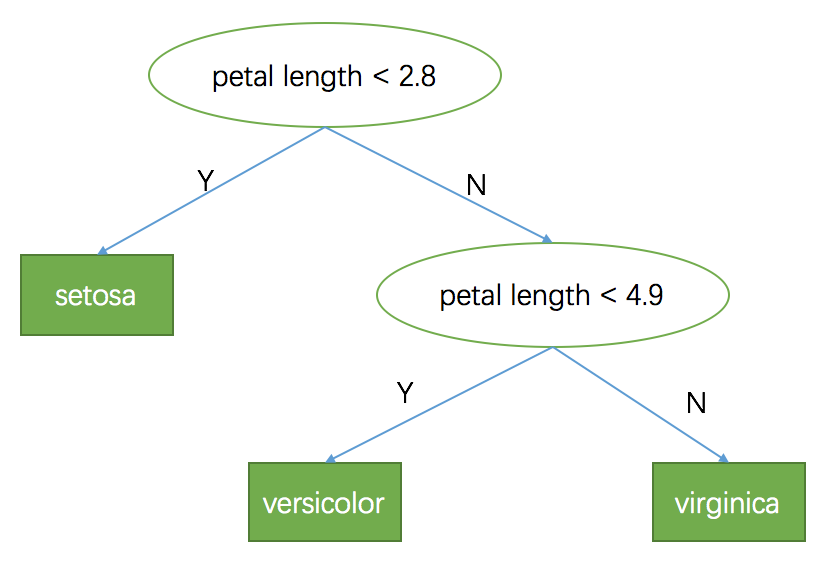
这个模型只用到一个变量,我们很自然想到,如果用更多变量,是不是可以预测得更好?没错,我们先看下第一个叶子节点(petal length < 2.8左子节点),被分到这个节点的样本有50个,都是setosa这个类别,所以已经100%分类准确了;再看下第二个叶子节点(petal length >= 2.8 && petal length < 4.9),这个节点里有49个样本,46个是versicolor,3个是virginica,但是我们的模型把这些样本都分类到versicolor这个类别,存在一定的分类误差。
那么,我们还能进一步提高分类的准确性吗?显然是可以的,很简单,对这个叶子节点上的49个样本,继续使用前面的分析方法,再选一个属性和阈值,将这49个样本继续划分成两个子集,那么准确率还能继续提升。
很容易想到,只要某个叶子节点上的样本不是同一个类别,都可以使用前面的方法一直划分下去,那么我们最终将会得到一个能几乎100%分类准确的决策树模型了!
# 决策树算法伪代码
def generate_decision_tree(D):
T = TreeNode() # 决策树
# 停止条件
if stop_critera(D):
return T
# 选择一个属性和对应的划分阈值,将数据集D分为D1和D2两个子集
attr, spliter, D1, D2 = select_attr_and_spliter(D)
T.value = (attr, spliter)
# 左子树
T1 = generate_decision_tree(D1)
# 右子树
T2 = generate_decision_tree(D2)
T.left = T1
T.right = T2
return T
对于一个样本集合D,先判断是否满足停止条件stop_critera,比如D中只有一个类别了,决策树就没必要继续生长了。然后选择一个数据和对应的划分阈值,将数据集分为两个子集。最后依次对这两个子集继续调用 generate_decision_tree 函数,生成左边的子树和右边的子树。
sklearn中的 DecisionTreeClassifier 实现了上述算法,因此我们可以直接调用这个算法,来实现鸢尾花识别模型。代码及解释如下:
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, export_graphviz
import graphviz
# 加载鸢尾花数据集
iris = load_iris()
# 创建决策树分类模型
clf = DecisionTreeClassifier()
# .fit函数执行了决策树分类算法,从数据集中学到了最优的分裂规则
clf.fit(iris.data, iris.target)
# 将决策树模型结构导出为pdf格式的图片
dot_data = export_graphviz(clf, feature_names=iris.feature_names,
class_names = iris.target_names,
out_file=None, filled=True)
dot = graphviz.Source(dot_data)
dot.render('iris')
load_iris 函数加载鸢尾花数据集,DecisionTreeClassifier()创建了决策树分类模型,但此时模型的决策树还是空的,因为还没有用数据训练它,我们调用决策树的.fit()函数,来执行决策树分类算法,执行结束后,决策树就生成了。后面的代码就是将决策树可视化显示出来,导出为 iris.pdf 文件,打开后可以看到决策树的结构如下:
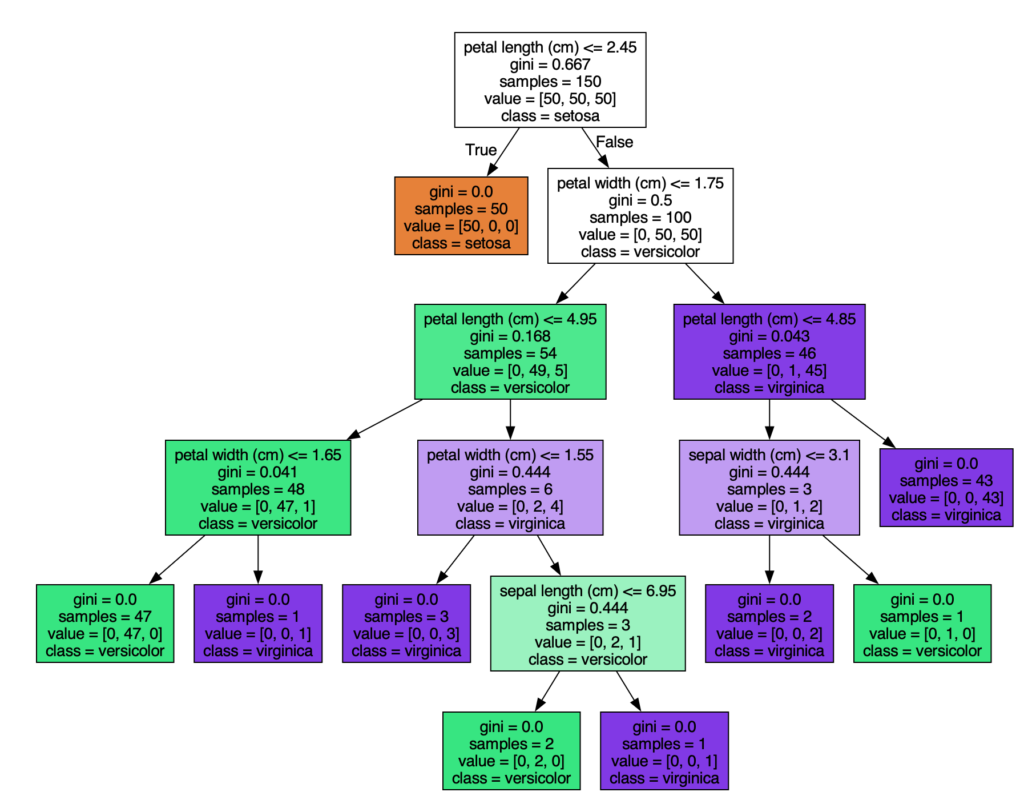
解释一下决策树上的信息,每个中间节点代表一个分裂规则,每个叶子节点代表一个最终的分类结果。samples是该节点的样本数,value表示三个类别的样本数,class表示这个节点最终判决的类别(即该节点上样本最多的类别)。
可以看到,叶子节点上,value的3个值只有1个非0,这表明叶子节点上只有一种类别的数据了,模型100%分类正确,所以叶子节点就停止继续分裂了,这就是前面的停止准则 stop_critera。
决策树模型和手写规则的区别
决策树模型可以看做一条条规则,前面单变量模型的规则非常简单,后面的多变量模型规则更加负责,但最终,我们发现每个叶子节点对应的规则,都可以用多个条件组合来描述出来。比如多变量模型中最左边的绿色的叶子节点可以写成:
petal length > 2.45 and petal width <= 1.75 and petal length <= 4.95 and petal width <=1.65那么,决策树模型岂不是跟手写规则没啥区别?
事实上,决策树模型跟手写的if…else规则本质上存在以下区别:
- 决策树模型的规则是从数据中拟合出来的,自动生成的;而手写规则是根据经验或数据分析总结出来的规则。
- 理论上决策树模型的规则比手写规则准确性会更高,实际问题中,决策树对应的规则也更加复杂,手写规则很难做到同等复杂度。
- 决策树的规则更加灵活,当数据发生改变时,不需要人工重新编写和调整规则,可以跟随数据变化,重新调用一下fit即可,灵活性更好。
动手实践
- 安装Python开发环境:安装配置python环境
- 安装sklearn软件包:
pip install scikit-learn
- 使用sklearn软件包,复现决策树分类算法的代码
- 决策树模型 DecisionTreeClassifier 有个max_depth参数,用于控制决策树的最大深度,设置这个参数的值为不同的值如2,4,6,观察一下生成的决策树的区别