回归树

1 回归问题
2 回归树
3 动手试试

回归问题

前面几章我们主要介绍了分类问题是怎么处理的，这一章我们要学习机器学习中另一类重要问题——回归问题。

回归问题是一种预测问题，其目标是根据给定的输入特征，预测一个连续的数值输出。与分类问题不同，分类问题的输出是离散的类别，而回归问题的输出是一个具体的数值。

以下是一些回归问题的例子：

房价预测：根据房屋的面积、房间数量、地理位置、房龄等特征，预测房屋的价格。这里的价格是一个连续的数值，可能从几十万到数百万不等。
销售预测：基于产品的历史销售数据、市场趋势、季节因素、促销活动等特征，预测未来一段时间内的产品销售量。销售量可以是任意的正整数。
股票价格预测：利用公司的财务数据、行业动态、宏观经济指标等，预测某只股票在未来特定日期的价格。股票价格是一个连续变化的数值。
气温预测：根据日期、地理位置、天气状况、季节等因素，预测某一天的气温。气温通常在一定的范围内连续变化。
油耗预测：根据汽车的型号、行驶速度、路况、载重等特征，预测汽车的油耗。油耗也是一个连续的数值。

在这些例子中，我们的目标都是通过输入的相关特征，建立一个模型来尽可能准确地预测出连续的数值输出。这类问题通常我没法通过前面用于分类的模型来解决，需要用到回归问题的专门模型。

在机器学习的领域中，回归树是一种强大而实用的工具。简单来说，回归树是一种基于树结构的预测模型，用于解决回归问题，即预测连续的数值型目标变量。

跟前面介绍的用于分类的决策树基本一样，也是一棵从根节点开始分裂，然后不断分裂生成的二叉树。但同时跟分类的决策树也有很多区别，下面我们就来详细介绍回归树。

我们还是以一个具体的例子加以说明。这个例子我们使用数据集sklearn中自带的Boston房价数据集。

Boston 数据集是一个用于回归分析的经典数据集，它包含了美国马萨诸塞州波士顿地区的住房价格相关信息。该数据集共有 506 个样本，具有 14 个属性，具体属性信息如下：

CRIM：城镇人均犯罪率。
ZN：占地面积超过 25,000 平方英尺的住宅用地比例。
INDUS：每个城镇非零售业务的比例。
CHAS：Charles River 虚拟变量（如果是河道，则为 1；否则为 0 ），用于回归分析。
NOX：一氧化氮浓度（每千万份），可作为一个环保指标。
RM：每间住宅的平均房间数。
AGE：1940 年以前建造的自住单位比例。
DIS：到波士顿的五个就业中心加权距离。
RAD：径向高速公路的可达性指数，反映距离高速公路的便利程度。
TAX：每 10,000 美元的全额物业税率。
PTRATIO：城镇的学生与教师比例。
B：1000×(Bk – 0.63)^2，其中 Bk 是城镇黑人的比例。
LSTAT：人口状况下降％，即低等收入阶层的人口比例。
MEDV：自有住房的中位数报价，单位为 1000 美元，这是需要预测的目标变量。

在这个任务中，我们要对每一个房屋样本进行预测。我们可以构建一个回归树来实现这个目标。首先，回归树会根据某个特征（比如房屋面积）来进行第一次分裂。例如，它可能会将数据分为“房屋面积小于 100 平方米”和“房屋面积大于等于 100 平方米”两个子集。然后，对于每个子集，它会继续选择其他特征进行进一步的分裂，直到达到某种停止条件（比如子集中的数据足够纯净或者达到了预设的树的最大深度）。

下面是回归树构建的伪代码，可以看到，跟决策树的总体逻辑没有太大差异。区别在于回归树的 select_attr_and_spliter 跟决策树不一样。

# 回归树算法伪代码
def generate_regression_tree(D):
    T = TreeNode()  # 回归树

    # 停止条件
    if stop_critera(D):
        return T

    # 选择一个属性和对应的划分阈值，将数据集D分为D1和D2两个子集
    attr, spliter, D1, D2 = select_attr_and_spliter(D)  
    T.value = (attr, spliter)

    # 左子树
    T1 = generate_decision_tree(D1)
    # 右子树
    T2 = generate_decision_tree(D2)

    T.left = T1
    T.right = T2
      
    return T

在决策树中，select_attr_and_spliter 是通过分裂后的两个子集的平均准确率来选择最优属性和分裂阈值的。那么在回归树中，该使用什么准则呢？

回归树中我们可以定义均方误差（MSE）来衡量准确率。对一个结点里的样本集合，我们定义均方误差为

$$ MSE = \frac{1}{n} \sum_{i=1}^n (y_i – \hat{y})^2$$

其中$\hat{y}$代表这个节点里，样本标签的平均值，在这个案例中就是落入这个节点所有房子的平均房价。可以看到，均方误差实际上就是房价的方差！方差越大，说明这个节点里面不同样本的房价差异很大，方差越小就说明房子的房价很接近。很显然，我们希望一个节点里面房价越相近越好，这样不同房价的房子就被回归树分到了不同节点，也就是说模型将不同房价的样本区分开了！

基于MSE，我们可以定义分裂后两个节点D1和D2的平均误差，D是分裂前的集合：

$$err = \frac{|D_1|}{|D|} * MSE_1 + \frac{|D_2|}{|D|} * MSE_2 $$

那么，我们就可以定义分裂准则为最小化平均误差err！套用深入理解决策树模型中的分裂算法，我们只需要改造一下 calc_split_value 即可！

def calc_split_value(D, D[attr], threshold):
    # 按照属性attr将D划分成两个子集
    D1 = [d for d in D if d[attr] <= threshold]
    D2 = [d for d in D if d[attr] > threshold]

    # 计算D1的准确率
    t1 = avg([d.target for d in D1])  # 计算D1中类别的平均数，作为D1集合预测结果
    r1 = avg([(d.target - t1)**2 for d in D1])  # 计算D1集合的MSE

    # 计算D2的MSE
    t2 = avg([d.target for d in D2]) 
    r1 = avg([(d.target - t1)**2for d in D2])

   # 计算平均误差
   r = (r1 * size(D1) + r2 * size(D2))/size(D)
   
   # 因为我们要最小化，所以加个符号
   return  -r

类似的，上面的所有流程，都可以使用sklearn轻轻松松实现，不用自己写代码。sklearn中的 DecisionTreeRegressor 实现了回归树算法。下面是使用它实现Boston房价预测建模的代码：

from sklearn.tree import DecisionTreeRegressor
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 加载波士顿房价数据集
boston = load_boston()
X = boston.data
y = boston.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

# 创建并训练回归树模型
regressor = DecisionTreeRegressor(max_depth=4)
regressor.fit(X_train, y_train)

# 在测试集上进行预测
y_pred = regressor.predict(X_test)

# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print("均方误差：", mse)

下面是这个回归树可视化后的结果

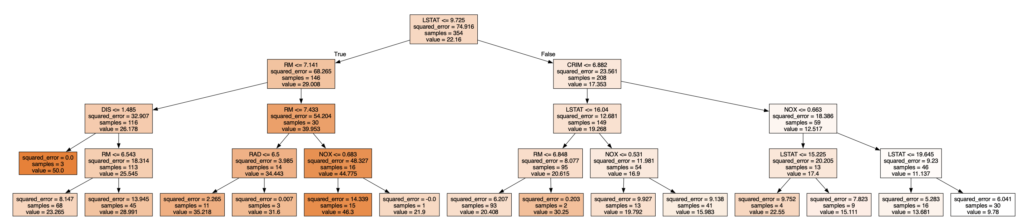
如果你在复现上述代码的时候，遇到错误，说Boston数据集不存在，那么可以替换 load_boston 为如下函数

def load_boston():
    import pandas as pd
    import numpy as np
    from collections import namedtuple

    feature_names = "CRIM,ZN,INDUS,CHAS,NOX,RM,AGE,DIS,RAD,TAX,PTRATIO,B,LSTAT".split(",")
    DataSet = namedtuple("DataSet", ["data", "target", "feature_names"])

    data_url = "http://lib.stat.cmu.edu/datasets/boston"
    raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
    data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
    target = raw_df.values[1::2, 2]
    return DataSet(data, target, feature_names)

好了，现在你已经学会用回归树来建模连续值预测的问题了！

动手试试

复现上述Boston房价建模任务，使用网格搜索找到最优模型！

浏览量: 87

回归问题

回归树

动手试试

实用机器学习