从前面使用决策树模型分类的经验中,我们可以发现,决策树模型最后几乎总是能100%预测准确!这说明决策树模型非常强大,复杂的任务也可以准确预测出来。但是我们也会有个疑惑,这样一个100%准确预测的模型应用到实际数据中,真的能全预测对吗?
模型的过拟合
为了验证上面的猜测,我们继续回到鸢尾花分类任务。
为了模拟实际情况,我们把数据集随机分为两份,一份我们可以用来训练模型,这部分数据通常是我们收集回来的,一份我们当做要解决的实际问题中的数据。比如,我们要做一个人脸识别系统,我们会先收集一批人脸数据,而在系统做好后,实际使用时,模型识别的数据都不在之前收集的数据里面。在机器学习领域,前一个集合我们用来训练模型的数据叫训练集,后一个数据集合我们叫测试集。
使用sklearn的 train_test_split 函数,我们可以轻松完成训练集和测试集的划分。
X代表用来预测的属性,在机器学习中我们叫特征;y代表要预测的类别,在机器学习中我们叫标签。test_size参数是划分的测试集比例,0.5即代表划分50%的样本当测试集。
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)现在,我们现在训练集上训练一个决策树模型
from sklearn.tree import DecisionTreeClassifier
# 创建决策树分类模型
clf = DecisionTreeClassifier()
# .fit函数执行了决策树分类算法,从数据集中学到了最优的分裂规则
clf.fit(X_train, y_train)训练好了之后,我们可以调用.predict函数预测训练集中的每个样本的类别,然后计算准确率。
import numpy as np
# 预测训练集的标签
y_pred = clf.predict(X_train)
# 计算准确率,结果应该是1,100%预测准确
print(np.mean(y_pred == y_train))接着我们再在测试集上计算准确率,结果发现准确率远低于1,只有0.5左右!
# 预测训练集的标签
y_pred = clf.predict(X_test)
# 计算准确率,结果应该是0.534
print(np.mean(y_pred == y_test))这是为什么呢?如果我们仔细分析上述流程,我们发现,模型是在训练集合上学到的知识,但是在测试集上有很多之前没见过的数据,所以就识别错了!这种现象,在机器学习里叫做过拟合!相反,如果模型在测试集上的性能非常好,跟训练集上几乎一样,那么我们就说模型的泛化能力强。
在机器学习中,过拟合现象是指模型在训练数据上表现得非常好,几乎完美地拟合了训练数据的特征和规律,但在面对新的、未见过的数据时,却表现得很差,预测准确性大幅下降。
具体来说,当模型过度专注于学习训练数据中的细节、噪声和特定模式,而忽略了数据中更普遍、更本质的特征和关系时,就容易发生过拟合。这可能导致模型变得过于复杂,包含了过多不必要的参数或规则。
关于过拟合,有个非常形象的类比。我们上学时经常遇到,平常做了很多习题,但是考试时遇到没做过的题还是不会做的情况,这就是过拟合!
过拟合的原因通常包括:训练数据量不足,使得模型无法学习到真正有代表性的模式;模型的复杂度太高,例如层数过多、参数过多等;训练过程中过度追求在训练数据上的高准确率,而没有考虑到模型的泛化到没有见过数据上的能力。
过拟合的解决方法
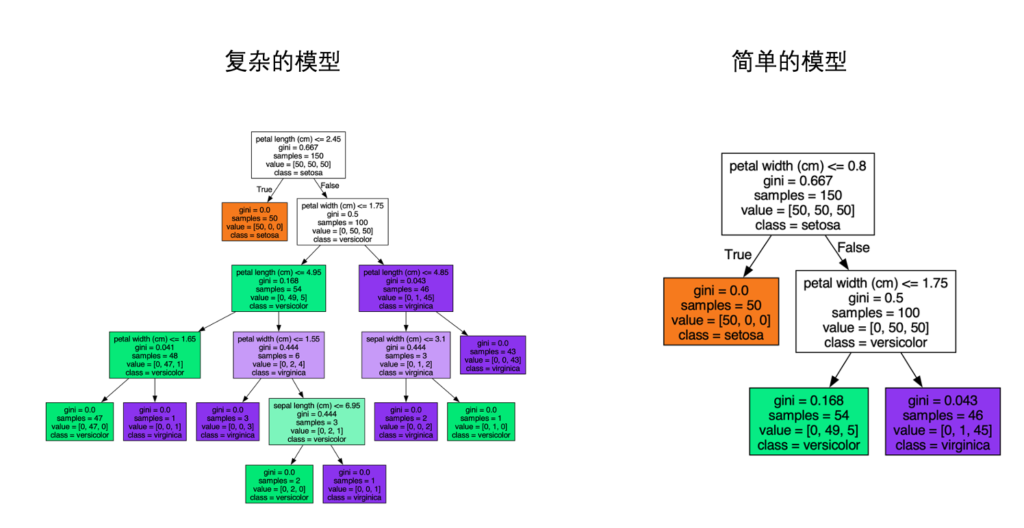
决策树模型可以通过限制树的深度来限制模型的复杂度,避免过拟合。通常更深的决策树模型(下图)更加复杂,也容易过拟合。限定决策树深度的方法很简单,我们在创建决策树模型的时候,指定 max_depth参数即可!
此外,我们还可以限定分裂的停止准则stop_critera,限定叶子节点样本数不能太少,这可以通过指定参数min_samples_leaf 来实现。
# 限定决策树最大深度是3,叶子节点上最少的样本数是5
clf = DecisionTreeClassifier(max_depth=3, min_samples_leaf=5) 最优参数搜索
上面我们说到,可以通过设置最大深度 max_depth 和 叶子节点最少样本数 min_samples_leaf 两个参数来控制模型过拟合。那么问题来了,我们怎么确定这些参数的值,或者说确定最佳值?
很简单,直接搜索。以最大深度为例,我们尝试系列深度值,从中挑选一个最优的就好了。最优的评估标准是,模型在测试集上的准确率最高。
如果有多个参数,那么我们就做多重遍历即可。以max_depth和min_samples_leaf 的参数搜索为例,算法如下:
best_params = (None, None) # 保存最优参数
best_acc = -inf # 保存最优参数对应的准确率
best_clf = None # 保存最优模型
for max_depth in range(1,10):
for min_samples_leaf in [1,3,5,10]:
clf = DecisionTreeClassifier(max_depth=max_depth, min_samples_leaf=min_samples_leaf)
# 在训练集上训练
clf.fit(X_train, y_train)
# 在测试集上评估模型的准确率
y_pred = clf.predict(X_test)
acc = np.mean(y_pred == y_test)
# 以测试集上的准确率来选择最优模型
if acc > best_acc:
best_params = (max_depth, min_samples_leaf)
best_acc = acc
best_clf = clf通常我们为了搜索效率,会只选择一部分可能得值和有限的范围去搜索。
上述搜索方法,如果把max_depth,min_samples_leaf放到坐标轴里,就像是在一个网格上去找最优参数组合,因此也被称作网格搜索(Gridsearch)。
sklearn软件包中提供了 sklearn.model_selection.GridSearchCV 可以帮助我们更高效地实现网格搜索。我们用这个函数改写上面的搜索算法如下:
from sklearn.datasets import load_iris
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
dtc = DecisionTreeClassifier()
# 设置参数的取值
params = {
"max_depth": range(1,10),
"min_samples_leaf": [1,3,5,10]
}
# 调用网格搜索
clf = GridSearchCV(dtc, params, cv=5)
clf.fit(iris.data, iris.target)GridSearchCV第一个参数是模型,第二个参数是参数配置,参数配置是一个字典,key是参数名,value是参数的所有可能的取值list。cv参数一个k-折叠数参数,通常选3-5即可。
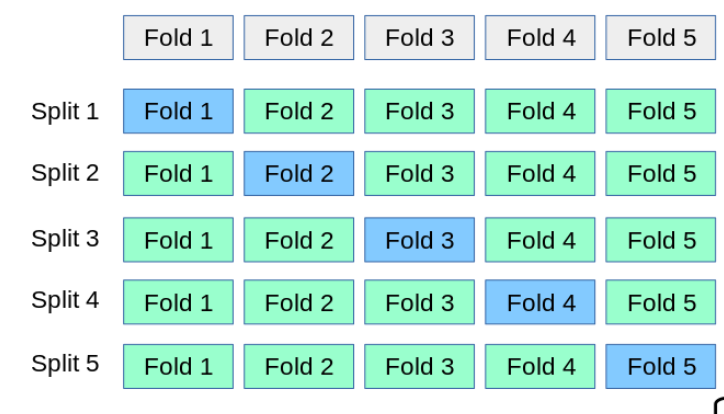
k-折叠是一种比我们前面简单划分训练集和测试集更科学的划分方式。如下图所示,是一个5-折叠划分示意图。一次划分(split)会将一个完整的数据集均匀分成5分,然后用其中4分用来训练模型,剩下的1分作为测试,用来评估模型的准确率。由于测试集有5种选择,所以可以跑5次评估流程,取个平均值来衡量这个参数组合的准确率,这样可以减少一定的随机性波动。
动手试试
改造一下之前的决策树模型,解决过拟合问题。然后验证解决过拟合问题后的模型,在测试集上的预测准确率更高!